nand2Tetris - Week 2 - Boolean Arithmetic and the ALU
Boolean Arithmetic and the ALU
This week, I built varipus types of adders and an Arithmetic Logic Unit (ALU). These components form the basis of arithmetic operations in digital systems.
Components Built
- Half Adder
- Full Adder
- Incrementer (Inc16)
- 16-bit Adder (Add16)
- Arithmetic Logic Unit (ALU)
Half Adder
The Half Adder is built using an XOR gate and an AND gate. Here is the truth table for the Half Adder:
| a | b | sum | carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
HDL Code
// Half Adder implementation
CHIP HalfAdder {
IN a, b;
OUT sum, carry;
PARTS:
Xor (a=a, b=b, out=sum);
And (a=a, b=b, out=carry);
}
Explanation
- The Half Adder takes two single-bit inputs and produces a sum and a carry.
- It uses an XOR gate for the sum and an AND gate for the carry.
Full Adder
HDL Code
CHIP FullAdder {
IN a, b, c; // 1-bit inputs
OUT sum, // Right bit of a + b + c
carry; // Left bit of a + b + c
PARTS:
HalfAdder(a=a, b=b, sum=sum1, carry=car1);
Xor(a=c, b=sum1, out=sum);
And(a=sum1, b=c, out=car2);
Or(a=car2, b=car1, out=carry);
}
Explanation
- The Full Adder adds three bits and produces a sum and a carry.
- It combines two Half Adders and an OR gate. Although I split the second Half adder into two of its components which is Xor And to make my process flow understand much better as it was tricky in the begnnning to come up with the logic.
Incrementer (Inc16)
HDL Code
// Inc16 implementation
CHIP Inc16 {
IN in[16];
OUT out[16];
PARTS:
Not(in=in[0],out=flip);
Or(a=flip, b=in[0],out=notIn);
HalfAdder(a=in[0], b=notIn, sum=out[0], carry=carry0);
HalfAdder(a=in[1], b=carry0, sum=out[1], carry=carry1);
HalfAdder(a=in[2], b=carry1, sum=out[2], carry=carry2);
HalfAdder(a=in[3], b=carry2, sum=out[3], carry=carry3);
HalfAdder(a=in[4], b=carry3, sum=out[4], carry=carry4);
HalfAdder(a=in[5], b=carry4, sum=out[5], carry=carry5);
HalfAdder(a=in[6], b=carry5, sum=out[6], carry=carry6);
HalfAdder(a=in[7], b=carry6, sum=out[7], carry=carry7);
HalfAdder(a=in[8], b=carry7, sum=out[8], carry=carry8);
HalfAdder(a=in[9], b=carry8, sum=out[9], carry=carry9);
HalfAdder(a=in[10], b=carry9, sum=out[10], carry=carry10);
HalfAdder(a=in[11], b=carry10, sum=out[11], carry=carry11);
HalfAdder(a=in[12], b=carry11, sum=out[12], carry=carry12);
HalfAdder(a=in[13], b=carry12, sum=out[13], carry=carry13);
HalfAdder(a=in[14], b=carry13, sum=out[14], carry=carry14);
HalfAdder(a=in[15], b=carry14, sum=out[15], carry=carry15);
}
Explanation
- The Inc16 increments a 16-bit number by 1.
- I used a series of half adders to increment the 16bit number by plus 1.
- It can be made with a simpler logic using Add16 also. Although it had a new syntax like b[0] = true, which I was unaware that it could be written in this way, so I used my own existing know-how and built is using HalfAdders.
16-bit Adder (Add16)
HDL Code
// Add16 implementation
CHIP Add16 {
IN a[16], b[16];
OUT out[16];
PARTS:
Not(in=a[0], out=flipA);
And(a=flipA, b=a[0],out=zero);
FullAdder(a=a[0], b=b[0], c=zero, sum=out[0], carry=carry0);
FullAdder(a=a[1], b=b[1], c=carry0, sum=out[1], carry=carry1);
FullAdder(a=a[2], b=b[2], c=carry1, sum=out[2], carry=carry2);
FullAdder(a=a[3], b=b[3], c=carry2, sum=out[3], carry=carry3);
FullAdder(a=a[4], b=b[4], c=carry3, sum=out[4], carry=carry4);
FullAdder(a=a[5], b=b[5], c=carry4, sum=out[5], carry=carry5);
FullAdder(a=a[6], b=b[6], c=carry5, sum=out[6], carry=carry6);
FullAdder(a=a[7], b=b[7], c=carry6, sum=out[7], carry=carry7);
FullAdder(a=a[8], b=b[8], c=carry7, sum=out[8], carry=carry8);
FullAdder(a=a[9], b=b[9], c=carry8, sum=out[9], carry=carry9);
FullAdder(a=a[10], b=b[10], c=carry9, sum=out[10], carry=carry10);
FullAdder(a=a[11], b=b[11], c=carry10, sum=out[11], carry=carry11);
FullAdder(a=a[12], b=b[12], c=carry11, sum=out[12], carry=carry12);
FullAdder(a=a[13], b=b[13], c=carry12, sum=out[13], carry=carry13);
FullAdder(a=a[14], b=b[14], c=carry13, sum=out[14], carry=carry14);
FullAdder(a=a[15], b=b[15], c=carry14, sum=out[15], carry=carry15);
}
Explanation
- The Add16 adds two 16-bit numbers and produces a 16-bit output.
- It chains multiple Full Adders to handle 16-bit inputs.
Arithmetic Logic Unit (ALU)
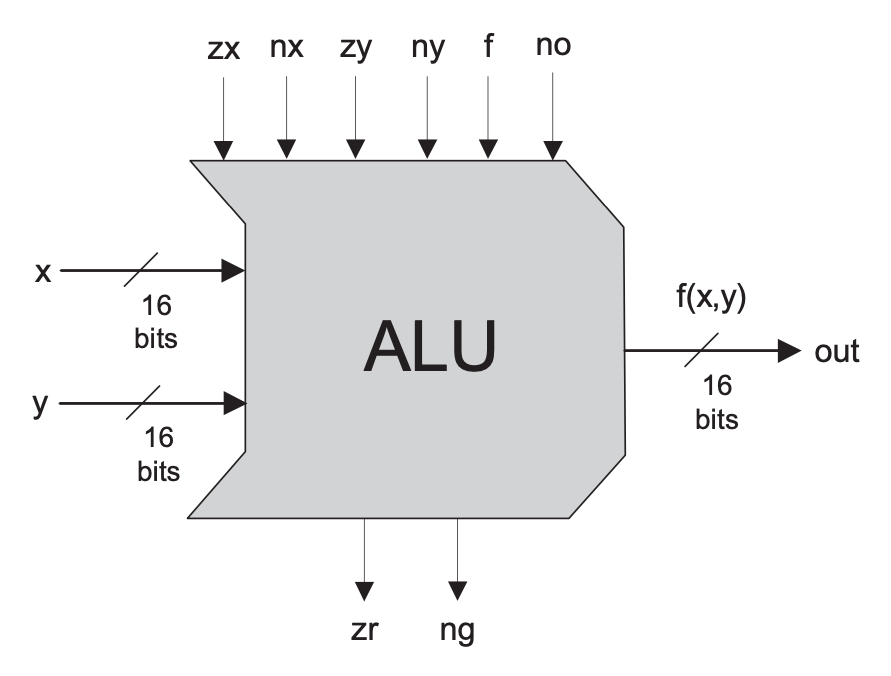
The ALU is one of the most critical components in digital systems. It performs arithmetic and logic operations. The ALU we built has multiple output pins to accommodate various functions like addition, bitwise operations, and more.
Diagram
HDL Code
// ALU implementation
CHIP ALU {
IN x[16], y[16], zx, nx, zy, ny, f, no;
OUT out[16], zr, ng;
PARTS:
// Implementation details using various gates and components
}
Explanation
- The ALU performs operations based on control bits (zx, nx, zy, ny, f, no).
- It has multiple outputs (out, zr, ng) to indicate the result and status flags (zero, negative).
- This highlights the need for multiple output pins to make the chip functional and versatile.
Conclusion
This week was challenging but rewarding. Building the ALU was particularly challenging as it was known to me that multiple output pins were necessary in the implementation of the chip, so it took more time than usual to problem solve. Getting stuck on a problem for hours and then solving it is indeed very rewarding, something I used to deprive myself off in the school years due to pressure of time during learning but I enjoy the problem solving now given that I have the freedom of time for solving the problems. Looking forward to building memory chips next week.